Noté como la palabra "mágicos" la dejaba instantáneamente obnubilada. En esta clase íbamos a jugar con números.
Pues bien, los cuadrados mágicos son distribuciones de números en celdas que se disponen formando un cuadrado, de forma que, la suma de cualquiera de sus filas, de cualquiera de sus columnas y de las dos diagonales principales da siempre el mismo resultado. Al número resultante se le conoce también como "constante mágica".
- Me recuerdan a los Sudokus - comentó ella, con un brillo de emoción.
No son exactamente Sudokus, pero sí se le parecen. Veamos a continuación un pequeño ejemplo de un cuadrado mágico de 3x3:
En este caso la constante mágica es 15, ya que esa es la suma que se produce en cualquiera de sus filas, de sus columnas y de sus diagonales (como hemos dicho más arriba). Fácil, ¿no?
Pues bien, os propongo los siguientes sencillos ejercicios:
1) En un cuadrado mágico de orden 3 (es decir, un cuadrado con tres filas y tres columnas, como el del ejemplo), coloca los números del 4 al 12 de forma que la constante mágica sea 24.
2) En un cuadrado mágico de orden 4 (esta vez tendremos cuatro filas y cuatro columnas) coloca los números del 1 al 16 de forma que la constante mágica sea 34.
3) En un cuadrado de orden 5, coloca los números del 1 al 25 de forma que la constante mágica sea 65.
Al final de la entrada os propongo un par de ejercicios más con cuadrados mágicos, pero un poco más difíciles. Por si tenéis sed de más.
Ahora vamos a pegarle un repaso a la trayectoria del cuadrado mágico. Porque lo mejor de este es que ha estado presente en nuestra historia, ¡sí, no somos los únicos locos que se entretienen con estas cosas!
Curiosidades e historia del cuadrado mágico
Estos cuadrados mágicos actualmente no tienen ninguna aplicación práctica a parte de la diversión de nuestra mente matemática. Sí que es verdad que a lo largo de la historia han estado presentes, sobretodo en aspectos relacionados a las supersticiones o la magia...
En China se conocían los cuadrados mágicos desde el III milenio a.C, y tienen una leyenda propia, atentos.
Según esta, cierto día se produjo el desbordamiento del río Lo; la gente, temerosa, intentó hacer una ofrenda al Dios del río para calmar su ira. Sin embargo, cada vez que lo hacían, aparecía una tortuga que rondaba la ofrenda sin aceptarla, hasta que un chico se dio cuenta de las peculiares marcas del caparazón de la tortuga, en el que había inscrito uno de los cuadrados mágicos. De este modo pudieron hacer la ofrenda con la cantidad que proporcionaba la constante mágica del cuadrado. Y así, se quedó el Dios satisfecho y volvieron las aguas a su cauce.
No obstante, el cuadrado mágico también se ha hallado en otras culturas, como la india, la egipcia o la griega, que le atribuían propiedades astrológicas y adivinatorias. Era frecuente grabarlo en talismanes.
La introducción de estos misteriosos cuadrados se le atribuye a Emanuel Moschopoulos (menudo nombre...) en torno al siglo XIV, que explica métodos para construirlos.
Sin embargo, estos cuadrados atrajeron la atención de grandes celebridades matemáticas (como Euler, Fermat, Pascal o Leibnitz), que estudiaron sus propiedades matemáticas (con un enfoque más científico) , a pesar de que son inútiles en la práctica.
Lo que demuestra, una vez más, que todo lo que suponga un reto para la mente, una manera de divertirnos, merece un poco de nuestro tiempo.
Aunque luego sea completamente inútil.
En particular, el cuadrado mágico que aparece en la imagen de arriba pertenece a Melancolía I, una obra de Alberto Durero (un señor considerado el primero de las artes europeas). Las dos cifras centrales de la última fila muestran el año de la ejecución de la obra. En la siguiente imagen podemos ver la totalidad de la obra. El cuadrado mágico está arriba, a la derecha.
Y el ejemplo más reciente se encuentra en la Catedral de la Sagrada Familia de Gaudí, ubicada en Barcelona. El cuadrado que hay en él tallado tiene como constante mágica el número 33 (la edad de Jesucristo en la Pasión), aunque también existe la teoría de que el número 33 se relaciona a una adscripción masónica.
Juegos con cuadrados mágicos
¿Y si todavía lo complicamos todo un poco más? Probad con los últimos cuadrados mágicos que os propongo, y ya me contáis que tal os ha ido. Estos no se los puse a mi pupila, claro. Estos van para vosotros. Ánimo y pensad, pequeños, pensad...
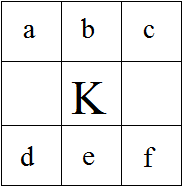
4) Y por último, hay que hallar el número K, sabiendo que el cuadrado mágico se compone por números del 10 al 18.
5) En este ejercicio solamente tenéis que completar el cuadrado mágico (recordad qué es lo que significaba que un cuadrado fuera mágico):
Soluciones
Espero que lo hayáis intentado antes... Antes de nada, no me matéis; pero estos dos últimos problemas no son demasiado triviales. Hay que coger boli y papel e intentarlo un poco más en serio. Evidentemente estos problemas no se los propuse a la niña; a ella se le puse todo un poco más fácil. La cuestión era que no me odiase, recordad...
4) Nos tenemos que ayudar con algunas letras para poder deducirlo:
Bastará con que sean las de las filas de arriba y abajo, pues nos darán suficientes datos para poder resolver el cuadrado.
Por las propiedades características del cuadrado mágico, sabemos que, si denotamos por N la constante mágica del cuadrado se cumple lo siguiente:
a+b+c=N
a+K+f=N
b+K+e=N
d+K+c=N
d+e+f=N
Sumando las tres igualdades centrales se tiene que:
(a+K+f)+(b+K+e)+(d+K+c)=3N
Y si reordenamos los sumandos:
(a+b+c)+3K+(d+e+f)=3N
Usando las igualdades de arriba que no hemos usado todavía, es decir, las sumas:
a+b+c=N
d+e+f=N
Se tiene que:
N+3K+N=3N
Y despejando la ecuación:
3K=N
Es decir:
K=N/3
Por tanto en número central K es un tercio de la constante mágica del cuadrado.
Por otra parte se sabe que los números que conforman el cuadrado mágico son los números del 10 al 18, es decir: 10, 11, 12, 13, 14, 15, 16, 17 y 18.
La constante mágica es la suma de todos los elementos del cuadrado mágico entre 3. Esto es fácil de comprobar, puesto que la constante mágica es el resultado de sumar los elementos de cada fila, de cada columna y de sus diagonales.
Por tanto:
10+11+12+13+14+15+16+17+18=126
Y por lo que hemos dicho antes, la constante mágica que hemos denotado con la letra N será la tercera parte de esta suma, es decir, N=126/3=42.
Y como K=N/3, se tiene que:
K=42/3=14.
¡Tachaaaaaaaan!
5) Ayudándonos del ejercicio 4 resulta ser bastante sencillo.
Antes de nada volvemos a rellenar los huecos convenientes con letras, de forma que:
Ahora ya podemos hacer operaciones parecidas a las que hacíamos. Por los visto en el ejercicio 4, la suma de cada fila y de cada columna es igual a 3K. Luego:
67+b+43=3K
b+K+73=3K
Que es un sistema sencillo de dos ecuaciones con dos incógnitas. Resolverlo es fácil, pero detallaré aquí los pasos para los que andeis perdidos todavía.
Despejando la primera ecuación en función de b se tiene que:
b=3K-110
Sustituyéndo esto en la segunda ecuación:
3K-110 +K +73 = 3K
K=37
Y como b=3K-110=3*37-110=111-110=1
Ya sabemos que la constante mágica es 3*K=3*37=111 (o bien al hacer la suma de los números que conforman la columna central, 1+37+73=111).
Rellenar los huecos ya es algo trivial, ¿no? Aquí os doy la solución:
¡Y además en este cuadrado mágico se tiene que todos sus números son números primos! ¿No es completamente genial?
Para saber más...
En los siguientes enlaces tenéis más sobre la historia y la construcción de los cuadrados mágicos, por si os habéis quedado con ganas de conocer más cosas acerca de ellos:
http://www.vicentetrigo.com/pdf/cuadrados.pdf
Los problemas los he sacado de la web:
http://platea.pntic.mec.es/jescuder/c_magico.htm
Los problemas los he sacado de la web:
http://platea.pntic.mec.es/jescuder/c_magico.htm










el 1 no es primo
ResponderEliminarHola! Es cierto que se trata de un tema bastante controvertido. Los matemáticos del siglo XIX lo consideraban así, y de hecho hay muchos teoremas enunciados bajo esta premisa. Sin embargo, como has indicado, últimamente no los consideran como tal... Todo depende de la definición de número primero que se utilice, como se desarrolla en el siguiente enlace:
Eliminarhttp://www.wikiprimes.com/el-1-es-primo/
Como ves, es una cuestión basada meramente en convención.
Un saludo y gracias!!
Te chuparia la concha
ResponderEliminar