Bueno, tengo que indicar que esta entrada participa en la Edición 6.6: números vampiro del Carnaval de Matemáticas, cuyo anfitrión este año es el blog Scire Science.
Después de haber contemplado el poder del número Φ en todo su esplendor en La divina proporción: girasoles, ciclones y galaxias, esta vez le tocaba a otro número mágico también en matemáticas, y que todo el mundo está habituado a usar.
- ¿Conoces el número Pi? -le pregunté al entrar en clase aquel día. Mi pequeña alumna lo piensa un poco antes de responder.
- Sí, este sí que sé cuál es. ¿Tiene algo que ver con los círculos?
En efecto, los círculos nos dan la clave que nos acercó al número Pi. Sin embargo, antes de adentrarnos en cómo surge el número Pi y dar algunos trazos sobre su historia y su aproximación es conveniente indicar que tanto el número Φ, como el número π pertenecen a un conjunto de números muy especial. Para entenderlo, veremos rápidamente qué tipos de números existen.
Los números irracionales
Para que se situase un poco mejor mi pupila, le dibujé en una hoja los siguientes conjuntos, usando distintos colores. Es importante saber que existen distintos tipos de números muy diferenciados. Dentro de cada conjunto he indicado algunos ejemplos de esos números.
 |
| Imagen 1: Tipos de conjuntos de números. |
El conjunto de los números reales, a su vez, se compone de números racionales y de números irracionales.
Los primeros son los que se pueden expresar como la fracción de un número entero (números sin decimales negativos o positivos) entre uno natural (números sin decimales positivos). Por ejemplo, 5/2 es un racional, pero también lo sería el -3, ya que se puede escribir como -3/1, o como -9/3; o también el número 5, que se puede expresar como 5/1, o como 10/2, etcétera.
Los primeros son los que se pueden expresar como la fracción de un número entero (números sin decimales negativos o positivos) entre uno natural (números sin decimales positivos). Por ejemplo, 5/2 es un racional, pero también lo sería el -3, ya que se puede escribir como -3/1, o como -9/3; o también el número 5, que se puede expresar como 5/1, o como 10/2, etcétera.
En particular el -3 sería entero, pero no natural, ya que este comprende únicamente los números mayores a cero, sin incluir a este; y el número 5 solamente sería natural. Bueno, dejo de enrollarme porque creo que queda bastante explicado en el diagrama.
Pero no nos descentremos: el grupo de números que nos interesa esta vez es el de los irracionales. Estos son los números que no se pueden expresar en forma de fracción. Incluyen las raíces cuadradas de algunos números, y números como el número π y el número Φ. Un rasgo que los caracteriza es que además de tener infinitas cifras decimales, estas cifras no siguen ningún tipo de patrón; es decir, no podemos predecir fácilmente el decimal que ocupa el puesto 300, o 1000 (a no ser que usemos un ordenador), y no digamos los decimales que ocupan un puesto todavía mayor.
Ah, se me olvidaba; además el número de números que componen cada conjunto es infinito, por supuesto. Y para rizar el rizo, los infinitos de cada conjunto de números son de distinto tamaño. Pero eso ya es otro tema. Quizás os interese el tercer vídeo que hay en la sección de vídeos de este mismo blog, donde se explican aspectos interesantes del concepto de infinito.
El número π
-Es una de las constantes mágicas más importantes, y se emplea en matemáticas, física e ingeniería -leyó pausadamente mi alumna, de la hoja que había llevado escrita.
Su valor es:
π = 3.14159265358979323846...
Puesto que es irracional, como hemos dicho antes, tiene infinitas cifras decimales. Por definición, π es la relación entre la longitud de una circunferencia y su diámetro. ¿Qué quiere decir esto?
Si se tiene un círculo de diámetro de 1 cm, entonces, la longitud de su perímetro es justo de 3.1415... cm. Si fuéramos capaces de cortar el círculo, y estirarlo hasta convertirlo en una línea recta, nos quedaría lo siguiente:
 |
| Imagen 2: Perímetro de un círculo. |
Pero seguro que lo entendéis algo mejor con la siguiente animación:
 |
| Imagen 3: wikipedia. |
Ante todo no hay que olvidar que el número Pi es la constante que surge al dividir el perímetro del círculo entre el diámetro de este. El número Pi también se considera una proporción, pues el perímetro de cualquier círculo es 3 veces su diámetro más un pedacito que es equivalente al 0.14... del diámetro. Es decir, que si en lugar de un diámetro de 1 cm, tenemos uno que mide 4 cm, el perímetro de este tendrá el valor 4 x π.
¿No os lo creéis? Os propongo que hagamos un experimento que leí por aquel entonces por los suburbios de internet y que me pareció del todo ilustrativo. Además, el experimento puede resultar muy útil para que los niños entiendan la importancia del número Pi en nuestra vida cotidiana.
Experimento
Yo se lo enseñé a la niña de esta forma y lo pasamos muy bien. Para llevarlo a cabo necesitamos una cuerda o cinta, una regla y un bote cilíndrico cualquiera que tengáis por casa. Qué ilusión, parece que vaya a hacer una de las manualidades imposibles de Art Atack... Pero nada más lejos de la verdad. No os ilusionéis. En mi caso el único bote que tenía a mano era uno de cola blanca, que no es completamente cilíndrico, pero da igual, porque solo voy a utilizar el círculo de la parte más ancha (de mayor radio).
¿No os lo creéis? Os propongo que hagamos un experimento que leí por aquel entonces por los suburbios de internet y que me pareció del todo ilustrativo. Además, el experimento puede resultar muy útil para que los niños entiendan la importancia del número Pi en nuestra vida cotidiana.
Experimento
Yo se lo enseñé a la niña de esta forma y lo pasamos muy bien. Para llevarlo a cabo necesitamos una cuerda o cinta, una regla y un bote cilíndrico cualquiera que tengáis por casa. Qué ilusión, parece que vaya a hacer una de las manualidades imposibles de Art Atack... Pero nada más lejos de la verdad. No os ilusionéis. En mi caso el único bote que tenía a mano era uno de cola blanca, que no es completamente cilíndrico, pero da igual, porque solo voy a utilizar el círculo de la parte más ancha (de mayor radio).
 |
| Imagen 4: Herramientas del experimento. |
Medimos con la regla el diámetro del bote:
 |
| Imagen 5: Medimos el diámetro. |
En mi caso concreto el diámetro mide aproximadamente unos 4.2 cm. Es difícil ser riguroso, sí que es cierto, pero bueno.
Por otro lado medimos el perímetro de la circunferencia, rodeando con la cinta el bote, así:
 |
| Imagen 6: Medimos el perímetro con la cinta. |
y haciendo una marquita. Luego colocamos la cinta sobre la regla para poder medir el perímetro de la circunferencia:
 |
| Imagen 7: Ponemos la cinta sobre una regla. |
Marca que el perímetro es de unos 13.2 cm.
Por lo que hemos visto antes, sabemos que el diámetro de un círculo por el número Pi, nos da el perímetro.
Por tanto debe ocurrir que 4.2 x π = 13.2, es decir, que 13.2/4.2 tiene que dar algo próximo a Pi (es muy difícil que dé exactamente el número Pi, pues nuestras mediciones no son extremadamente exactas, pero sí debe dar algo bastante aproximado, aviso).
Si hacéis la división, en efecto el resultado da 3.142857... Que solo coincide con pi en los dos primeras cifras decimales (pero este error se debe a lo que he mencionado antes, las mediciones no las hemos hecho con precisión milimétrica). Con una medición ajustada al 100%, obtendríamos el número Pi.
Probad a hacerlo vosotros en casa con cualquier otro bote, y al dividir su perímetro entre su diámetro, ¡debe dar siempre lo mismo!
Orígenes del número π
Como supongo que ya intuís, esta constante se descubrió hace bastante tiempo. Ya en la antigüedad, se insinuó que todos los círculos conservaban una estrecha dependencia entre el contorno y su radio. Pero no fue hasta el siglo XVII que no se convirtió en un dígito, y se identificó con el nombre de "Pi", que viene de la palabra "periphereia", que es como denominaban los griegos al perímetro del círculo.
Esta notación fue usada por primera vez en 1706 por el matemático galés William Jones y popularizada por el matemático Euler en su obra "Introducción al cálculo infinitesimal" de 1748.
El valor de esta constante mágica ha sido conocida con diferentes precisiones en el curso de la historia:
- En una de las referencias documentadas más antiguas, como lo es la Biblia, aparece de forma indirecta asociada con el número 3.
- En Mesopotamia, los matemáticos la empleaban como la aproximación de 3 más un octavo.
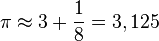
- Un coetáneo de Sócrates, Antiphon, inscribió en el círculo un cuadrado, luego un octógono e ideó multiplicar la cantidad de lados hasta el momento en que el polígono obtenido ajustara casi con el anillo.
 |
| Imagen 8: web.calstatela |
- Euclides precisa en sus Elementos los pasos al límite necesarios e investiga un sistema consistente en doblar, al igual que Antiphon, el número de lados de los polígonos regulares y en demostrar la convergencia del procedimiento. Un esquema de cómo funcionaría hoy el paso al límite puede ayudar a comprender, por ejemplo, por qué el área del círculo es el producto de Pi por el radio al cuadrado.
 |
| Imagen 9: Libro "Los secretos del número Pi". |
- Arquímedes reúne y amplía estos resultados. Prueba que el área de un círculo es la mitad del producto de su radio por la circunferencia y que la relación del perímetro al diámetro está comprendida entre 3,14084 y 3,14285.

Imagen 10: wikipedia.
- En el siglo II d. de C., Ptolomeo utiliza polígonos de hasta 720 lados y una circunferencia de 60 unidades de radio para aproximarse un poco más, y da el valor 3 + 8/60 + 30/3600 = 377/120 =3.14166... ¡Parece que ya se parece más al número que conocemos hoy en día!
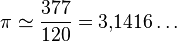
- El cálculo de Pi atrajo la atención a matemáticos expertos de todas las culturas. Hacia el año 263, el matemático chino Liu Hui fue el primero en sugerir que 3,14 era una buena aproximación, usando un polígono de 96 o 192 lados. Sin embargo a él no le parecieron suficientes lados y decidió superar esa aproximación empleando un polígono de nada más y nada menos... ¡3072 lados!
 |
| Imagen 11: wikipedia. |
- A finales del siglo V el matemático y astrónomo chino Zu Chongzhi calculó el valor de π en 3,1415926, al que llamó «valor por defecto», y 3,1415927, «valor por exceso», y dio dos aproximaciones racionales de π, 22/7 y 355/113, muy conocidas ambas, siendo la última aproximación tan buena y precisa que no fue igualada hasta más de nueve siglos después, en el siglo XV. ¡Qué máquina!
- A partir del siglo XII, con el uso de las cifras arábigas en los cálculos, se facilitó mucho la posibilidad de obtener mejores cálculos para Pi.
- Uno de los casos más curiosos de la historia fue el del matemático inglés William Shanks, quien, después de un trabajo que le llevó casi veinte años, obtuvo 707 decimales en 1853. Desgraciadamente, Shanks incurrió en un error en el 528º decimal, y a partir de éste están todos mal. Pobrecillo.
El número π en la era computacional
Desde el diseño del primer ordenador se empezaron a desarrollar programas para el cálculo del número π con la mayor cantidad de cifras posible. De esta forma, en 1949 se pudieron obtener 2037 cifras decimales en 70 horas.
En la década de los 2000, los ordenadores ya son capaces de obtener números que poseen una inmensa cantidad de decimales. En concreto en 2009 se hallaron más de dos billones y medio de decimales de pi mediante el uso de una supercomputadora, compuesta por 640 computadoras de alto rendimiento, que juntas consiguen velocidades de procesamiento de 95 teraflops. Lo obtuvieron en 73 horas y 36 minutos.
Los últimos datos que se tienen indican que en 2011 se batió el último récord, de mano de Shigeru Kondo, que ya ha descubierto las 10 000 000 000 000 primeras cifras del número Pi.
 |
| Imagen 13: Aula Geek. |
Locas y absurdas curiosidades
Como sé que os gusta saber estas cosas también os contaré algunas curiosidades de este mágico número. Sabías que...
1) ¿El día de este número es el 14 de Marzo? El día 14 del mes 3: 3,14...No es demasiado conocido, pero cuentan que... Ese día suelen ocurrir cosas buenas. No, ahora en serio. Solo los verdaderos amantes de este número llaman a sus amigos para felicitar este día. Se puede entender como un pequeño tributo para este número tan maravilloso.
2) ¿Se hacen, hoy en día, concursos de microrrelatos con el número Pi?
Sí, sí; lo estas escuchando bien. Tomando las primeras cifras del número Pi (por ejemplo las 20 primeras), se compone el microrelato, de modo que, si recordamos:
π=3.1415926535897932384...
la primera palabra tendrá 3 letras, la segunda, 1, la tercera 4, etcétera...
Esta clase de concursos fue pionero en la universidad de Alicante (universidad en que servidora estudió), en la Facultad de Ciencias, y en el siguiente enlace podéis ver con vuestros propios ojos en qué consiste:
En particular, la ganadora de la edición de 2013 fue la siguiente:
“Voy a casa y busco recuerdos. La mañana llega sin tener consuelo. Solamente intento continuar sin tu luz, anhelado amor”.
3) ¿Hay gente por el mundo que le ha puesto música al número Pi, asignando a cada cifra decimal una nota musical? ¡Todos locos!
4) ¿Hay chistes muy malos en los que se ve implicado?
 |
| Imagen 12: Chiste Pi - ojo |
 |
| Imagen 13: Pájaro Pi. |
Bibliografía
Hay multitud de sitios webs y libros que tratan sobre el número Pi.
Algunos sitios que he consultado son los siguientes:
Algunos sitios que he consultado son los siguientes:
También he consultado este libro:
"Los secretos del número π, ¿Por qué es imposible la cuadratura del círculo?", Juaquín Navarro.